Product Quantization in Postgres

Embedding dimensions and index memory

Embedding models are powerful tools in machine learning that transform text, images, or other data types into vectors. These vectors, known as embeddings, capture the essential features and relationships within the data. The quality of an embedding model is influenced by several factors, including the amount and quality of training data, the size and architecture of the model, and the dimensionality of the embeddings produced.

While higher-dimensional embeddings can represent more nuanced relationships and features, they also come with increased computational and memory costs. This can affect practical applications, such as vector search. Indexes are a way to make vector search queries more efficient. However, high-dimensional vectors can pose a problem for vector indexes.

Fitting the index in-memory can be expensive. In an earlier blog post, we provide an interactive calculator to help understand the memory requirements of an index. For example, an index on 100M 768-dimensional vectors requires about 300GB of memory. On GCP, this costs over $2400 / month with a machine like c3-highmem-44.

Storing the index on disk instead of in-memory can reduce costs, but also leads to slow queries due to disk I/O. For example, Qdrant ran benchmarks that found queries per second decreased from almost 800 to 50 with optimized hardware.

Moreover, in Postgres, indexes over large vectors are difficult to support. Indexes are stored in 8kB sized pages. The largest vector that can fit on one page is about 2000 dimensions. It is possible to support larger dimensions, but at the cost of increased complexity and reduced performance. As a result, Postgres vector search extensions like pgvector and Lantern currently only support up to 2000 dimensions for vector indexes.

What is product quantization?

One way to address the index size problem is with compression. In this article, we’ll focus on product quantization (PQ), which is a compression technique for high-dimensional vectors.

PQ works in a few steps:

1. Clustering: We divide each vector into equal-sized subvectors. For each set of subvectors, we run the k-means algorithm to identify centroids, or representative subvectors, for that subspace.
2. Quantization: For the stored vectors, we quantize each subvector by encoding it with the ID of the nearest centroid and store this quantized representation in a column.
3. Indexing: We use the quantized vectors to generate an HNSW index. Inside the index, we store the centroid IDs for each subvector.
4. Searching: When a query vector is submitted, it traverses the index structure by calculating the distance between the original query vector and the quantized database vectors.

The diagrams below depict an example of this process. In this example, we calculate 256 centroids for each subvector of length 32. This results in over 99% memory reduction.

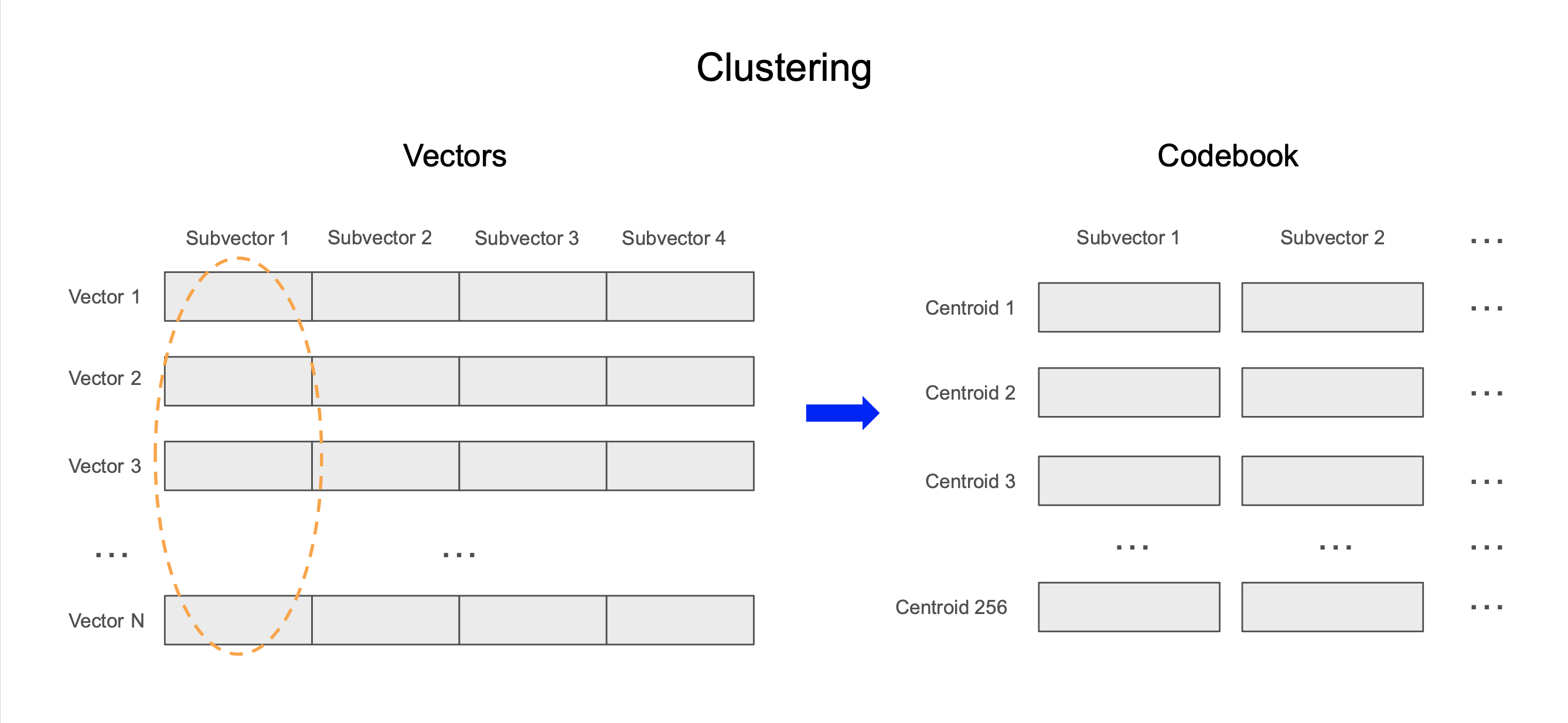
Clustering: We divide each 128-dimensional vector into 8 equal-sized subvectors. For each set of 16-dimensional subvectors, we compute 256 centroids using the k-means algorithm and store these in a “codebook”.

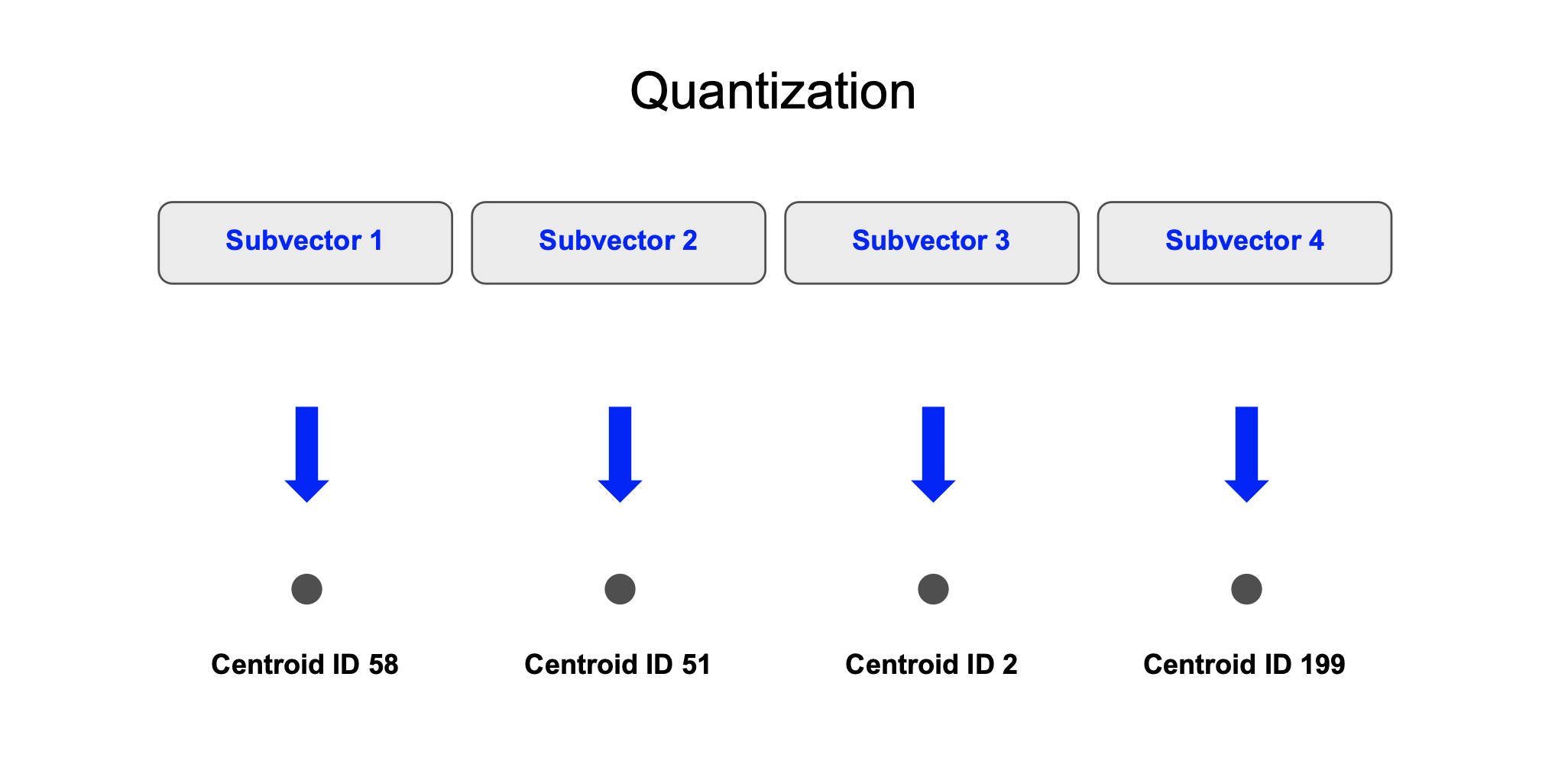
Quantization: We compute the quantized version of each 128 dimension vector. For each of the 8 subvectors, we determine the centroid and store the centroid’s ID. Since there are 256 centroids, each ID can take up 8 bits.

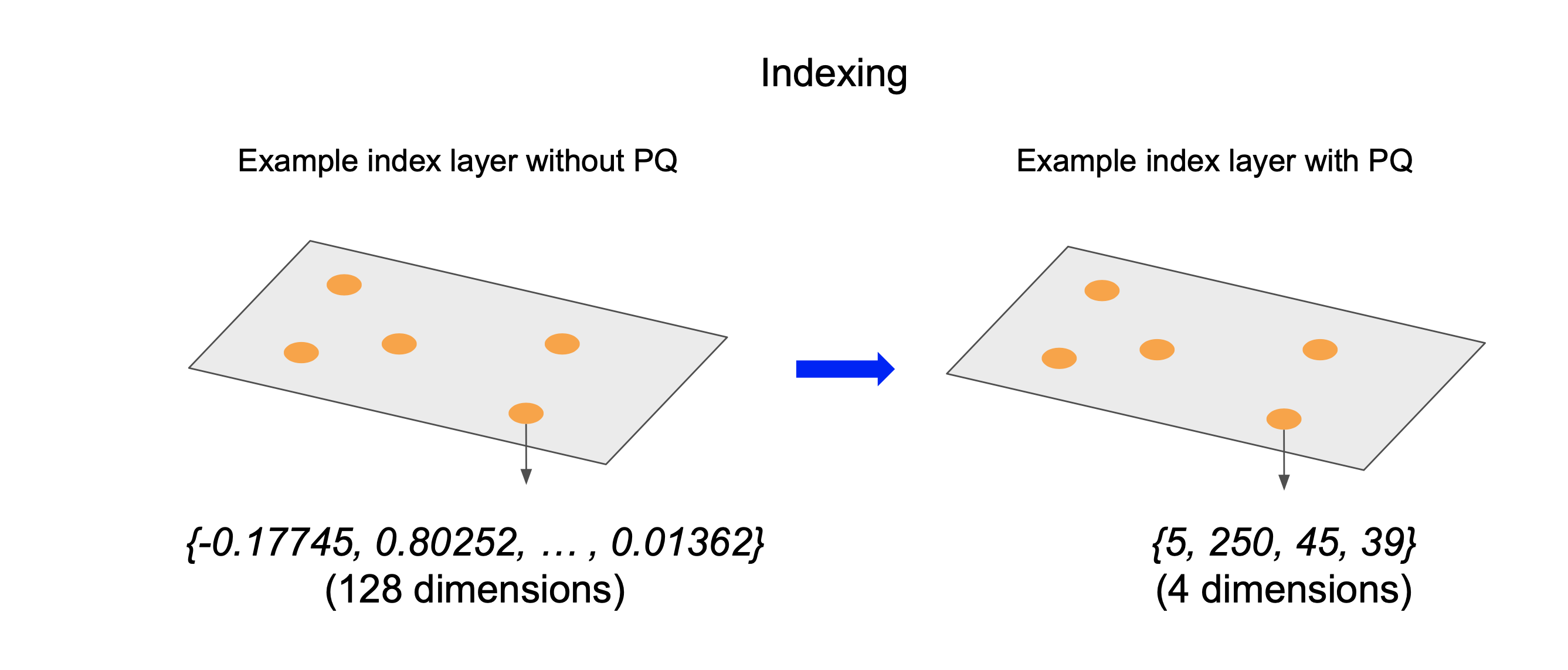
Indexing: We use the quantized vectors to generate an HNSW index. Note that this has less memory requirements than the non-quantized HNSW index, since we store centroid IDs as opposed to full vectors.

It’s important to note that PQ is a lossy compression technique, meaning that some information is lost during the compression process. This loss can affect the recall of the search, as the compressed vectors may not perfectly represent the original data. As a result, it’s important to experiment with compression parameters to determine acceptable recall-latency tradeoffs. We can also mitigate this using techniques such as rescoring with the original uncompressed vectors.

How we implemented PQ in Postgres

At Lantern, we’re building a suite of tools to support AI applications in Postgres. We added support PQ to our core Postgres extension, and also to our CLI, which enables using resources external to the database for better performance.

Clustering and quantization

We implemented clustering and quantization for a table in SQL, which accepts a table, column, number of clusters, length of subvector, and distance metric as parameters. The query below generates a column v_pq of PQ vectors using 50 clusters and length 32 subvectors.

SELECT quantize_table('sift_base1k', 'v', 50, 32, 'l2sq');

For larger datasets, to take advantage of multiple cores, use the CLI

lantern-cli pq-table --uri 'postgresql://[username]:[password]@localhost:5432/[db]' --table "sift1m" --column "v" --clusters 256 --splits 32

This can be run locally, and can be parallelized across GCP batch jobs using the --run-on-gcp parameter. We note that for parallelism, the data should have an ordered BTREE index, so that the data can be split into chunks, and that the database should be able to handle the number of connections.

Quantization

We support encoding each vector using an 8-bit unsigned integer type. This allows us to support up to 256 distinct centroids, as each centroid can be assigned a unique identifier ranging from 0 to 255.

Since Postgres does not have a native one-byte integer type, to store PQ vectors we created the PQVEC type which stores one byte for each element in the encoded vector, allowing for efficient storage of quantized vectors.

We support subvectors of length ranging from 1 to D, where D is the dimensionality of the vector. It is important to ensure that the length of your overall vector is divisible by the length of the subvectors. Note that a subvector of length 1 is a special case of product quantization called scalar quantization.

We store the subvector and centroid information in a structure called a “codebook”. The cookbook is a table with columns (subvector_id, centroid_id, centroid_vector). The subvector_id will indicate an index of the subvector.

Indexing

Index creation is supported inside SQL using a CREATE INDEX command like the following (see documentation here).

CREATE INDEX USING lantern_hnsw (embedding dist_l2sq_ops) WITH (m=16, ef_construction=128, ef=128, dim=768, pq=true);

By passing pq=true, Lantern looks for the codebook generated for the vector column by the clustering and quantization steps.

We also support creating the index externally using the Lantern CLI (see documentation here). This is written in Rust. This allows the index creation process to take advantage of multiple cores and offload the expensive index creation process from the database.

lantern-cli create-index \
    --uri 'postgresql://username:password@localhost:5432/db' \
    --table "books" \
    --column "embedding" \
    -m 10 \
    --efc 128 \
    --ef 64 \
    --metric-kind l2sq \
    --out /tmp/index.usearch \
    --remote-database
    --pq
    --import

Searching

If a PQ index is created on a column, then vector searches will automatically use the PQ index as long as the Postgres planner determines that using the index will save query time.

SELECT id FROM books WHERE embedding <-> ARRAY[1.0,2.0,3.0] LIMIT 1;

During search, the original non-quantized query vector is compared against quantized vectors in the HNSW index to find the closest vectors. The PQ index adds an additional computation cost since it requires de-quantizing vectors during search. However, this cost is in practice negligible due to high-performance SIMD-accelerated vector operations in Lantern, inherited from usearch.

Benchmarks

Setup

We ran benchmarks using a fork of the VectorDBBench vector database benchmarking suite, which adds support for Lantern, product quantization, and fixes issues with Postgres vector search. To read more about our fork, see [here].

For our dataset, we used 100M 768-dimensional embeddings from the LAION2B vector dataset included in VectorDBBench. These are image embeddings generated using CLIP.

We performed product quantization by generating a cookbook using a 10M subset of the 100M vectors. We used subvectors of length 4 and calculated 256 centroids per subspace using k-means with maximum iterations 20 and maximum tolerance 0.1. This took ~4.5 hours to run using 10 96vCPU machines.

The final size of the index was ~50GB, and represented a 6x reduction in memory compared to an uncompressed index, which is around ~300GB. (The size of the vectors in the index is reduced by 16x; the other large contributor to index size is the neighbor list, which is not reduced by PQ).

The database server had 32vCPU, 200GB RAM, and 80GB shared buffers.

Index construction took ~12 hours with (m=16, ef_construction=128, ef=128) on a 44vCPU machine with SIMD enabled.

Results

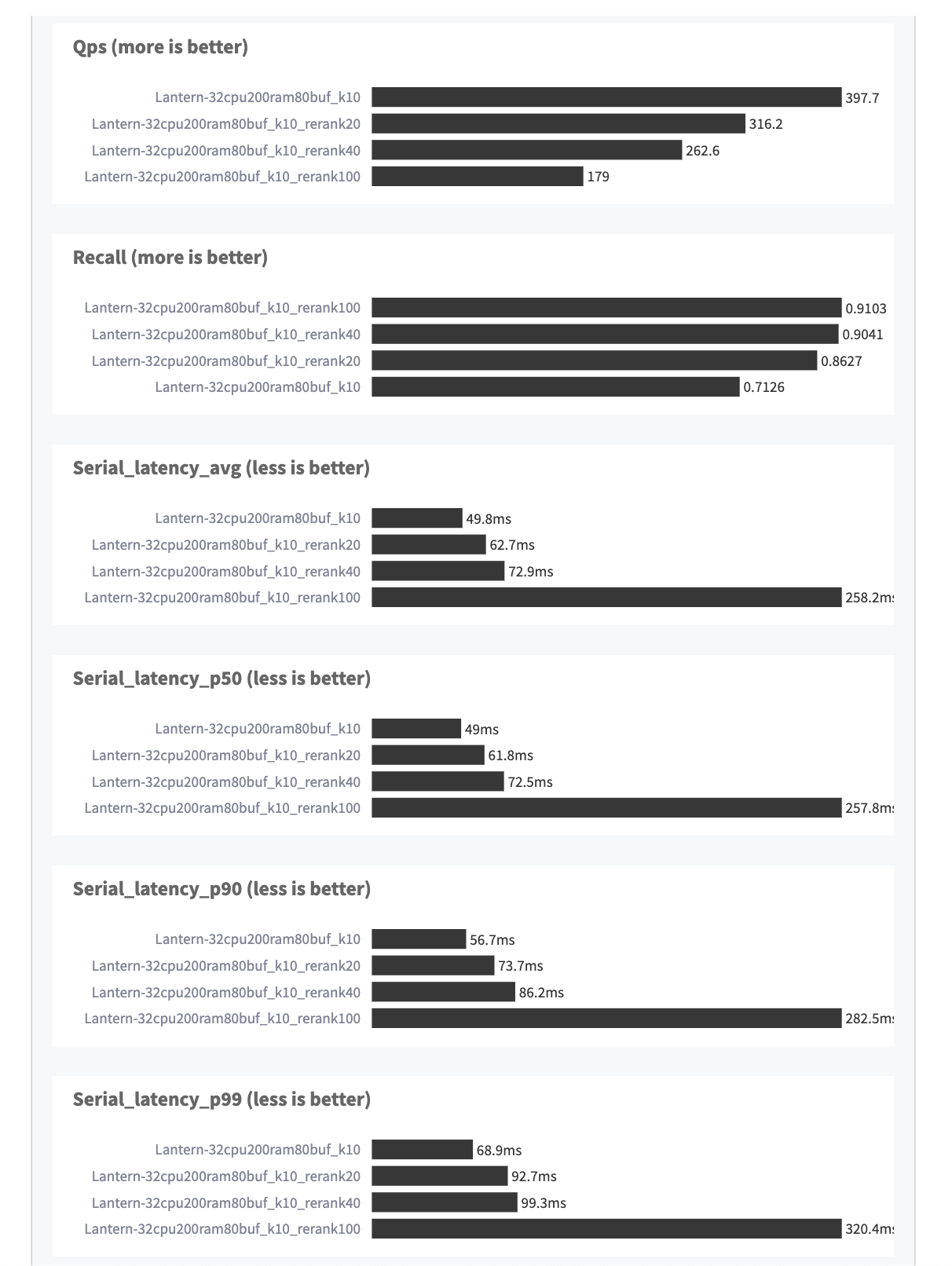
Some highlights:

• Recall@10 was 0.71 with 50 ms median latency.
• With re-ranking over 40 items, recall@10 was 0.90 with 73 ms median latency.

Conclusion

In this article, we showed how product quantization (PQ) is a valuable technique to address the problem of index size that comes with a large collection of high-dimensional vectors. By compressing the vectors via clustering and quantization, PQ significantly reduces memory requirements while maintaining search quality.

We implemented PQ in Postgres and benchmarked our approach using LAION’s 100M image embedding dataset. We were able to achieve 90% recall with under 100 ms median latency.

Our source code is available at lanterndata/lantern, lanterndata/lantern_extras, and lanterndata/vectordbbench.

If you have any questions or feedback for us, we’d love to hear from you. Please feel free to reach out at support@lantern.dev.